SYNDEX NUMBER DYNAMICS
(c)2010, Iona Miller; All Rights Reserved; Use with Permission Only
SYNDEX - NUMBER HARMONICS, RESONANCE & DYNAMICS
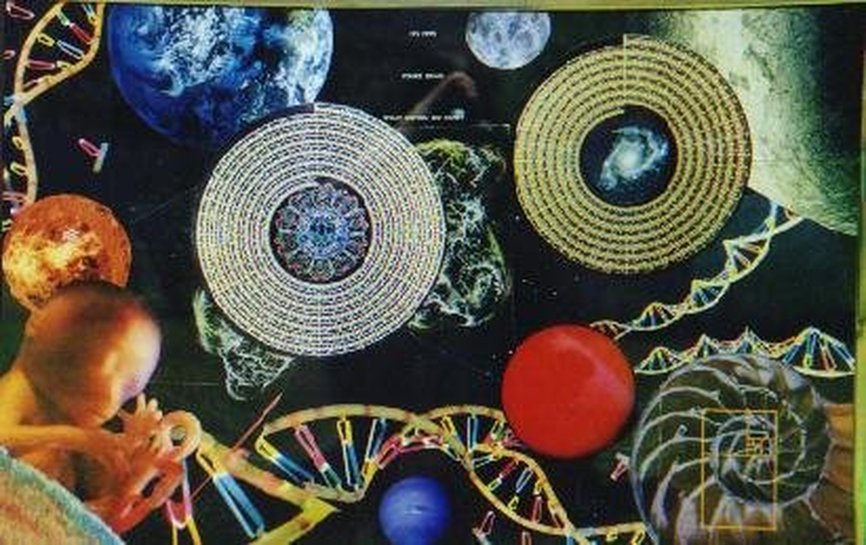
SYNDEX NUMBER DYNAMICS
- THE AURIC KEY: SYNDEX SYNOPSIS, (©1999)
- SYNDEX I: A Synergetic Perspective on Number Dynamics, (©1998)
- SYNDEX II: A Synergetic Revisioning of Number Dynamics
In Light of Ancient Metrology and Modern Cosmography, (©1999)SYNERGETICS LINKS
Syndex I & II are about the spiritual and universal beauty of numbers. They reflect the order and beauty of nature, but also of psyche. According to Jung, number unifies the physical and psychic (as in "realm of the psyche", not fortunetelling) worlds through synchronicity. Jung's basic ideas about the unity of knowledge and existence are in principle synonymous with the Platonic tradition, alchemy, Qabala and Gnosticism. Plato treated the end product of the evolution of mathematical concepts, (a fixed system of idealized objects), as an independent beginning point of the evolution of the "world of things." This concrete form of philosophy was determined by the nature of Greek mathematics. These philosophies seek to reconcile the actual condition with a hypothetical distant ideal, which expansively incorporates both personal and universal dimensions. It is an inward-oriented epistemology. By intuitive perception we can consciously reiterate the laws of Nature and mind which are equivalent to the archetypes themselves. Belief in the essential aspect of the mathematical as a real world, a "last reality" underlies the surprising efficiency of mathematics in the natural sciences and technology.
But are numbers really abstract entities existing independently of the human mind? What is the nature of mathematical truth, and how is it translated into mathematical knowledge? If it exists in another "ideal world", how can we know anything at all about the subject-matter of mathematics? What collective criteria determines the nature, terms and rules of this world?
In the Jungian view, numbers (like other archetypes of the collective unconscious) are contents and patterns of behavior which are not personally acquired in experience but are inborn. The Platonic Forms are the objects of knowledge, which is regarded as innate. They can emerge dynamically as well as imagistically. The essential nature of the Forms is dual: unity and multiplicity, finitude and infinitude. "The One" is the origin of Forms in the same way that the psyche is the origin of the archetypes.
Because they form a primary conceptual language, numbers have heavily influenced the development of culture, philosophy and myth as well as sciences such as cosmology. 'Number is All' was the Pythagorean motto. Numbers were symbols representing cosmic principles. The whole philosophy of numbers came from distinctions created by the primordial division of the One into multiplicity. Because of their archetypal essence, their mode of articulation is essentially mythic and radically symbolic.
Mathematics, by the very nature of its method, is an essentially Platonic pursuit. Mathematicians treat the objects of their investigations as real objects in a hypostasized space, as if they existed independently in some pure world of their own. Thus, they reason that the amount of prime numbers is "infinite." Discussing the amount of prime numbers, mathematicians believe that they are discussing objects as real as collections of things in their everyday life.
We use numbers casually and rigorously as a language to order space. Since ancient times, their archetypal dynamics have been the foundation of philosophy, religious, and artistic thought. Patterns of dynamic energy in numbers reflect patterns of nature--the order of the universe. Whether they actually form the basis of the universe is the subject of ongoing debate among many schools of mathematicians. The qualitative distinctions we make between phenomena are fundamentally numerical. We still don't know why the universe appears to follow mathematical laws. However, as Hilbert has suggested, we do know that the idea of the Infinite deviates significantly from the situation in the physical Universe.
Are numbers and functions the inventions of mathematicians, or do they exist independently of us? Just because a mathematical object can possibly exist doesn't mean it actually does exist. Yet, mathematicians imagine they are talking about real objects, when they may be talking about stabilized concepts. The new direction in the philosophy of mathematics is a "quasi-empirical approach that treats mathematics as just another messy experimental science." A partially unconscious process of idealization ends in the stable concept of numbers, points, lines, spheres.
When working in geometry, a mathematician does not investigate the relations of real things. He investigates some idealized, fixed notion of these relations. This notion is subjectively treated as "reality" without any fundamental reality behind it. It can, therefore, arguably be considered art as well as science. In practice, mathematicians jump to conclusions, and after the jump has been made begin the labor of proving the theorem or constructing a coherent theory. This involves subconscious reasoning, tenacity, focus, judgement, concentration, elementary intuition, free association, and conceptual visualization.
Some say mathematics is a purely human construct, an artifact of our nervous systems and culture. Others attest that even chimps and infants are hard-wired by evolution for arithmetic to deal with real objects in the real world. Numbers are not Platonic ideals but neurological creations. Integers, like colors, are artifacts of our sensory processing mechanisms.
Dehaene traces the arithmetical model to the inferior parietal cortex. This poorly understood location is where visual, auditory, tactile signals, and language processing converge. Mathematics, or at least mathematical notation, is another human languge. It also appears to be the language of nature, and therefore physical reality. Of the infinite range of mathematical creations, scientists keep those that help explain and predict reality.
The concept of natural numbers is a fixed model, an idealization of quantitative relations which ends in stable concepts of numbers. The dynamics of those numbers are described in number theory. Number theory, one of the oldest branches of pure mathematics, concerns elementary properties of primes, divisibility among integers, the existence of greatest common divisors, the study of specific families of numbers, simple recurrent relations, factorization, and more. Syndex addresses these aspects with easy to state conjectures which can be understood and observed in graphics without any particular mathematical training.
Mathematical Platonism concerns the investigation of fixed or self-contained models. The Platonic Idea or Form is essentially an unchangeable form. As symbols, numbers express the particular in the universal, the eternal in the finite. They express the ordering function of their archetypal nature. The Neoplatonists assumed an a priori structure of knowledge grounded in archetypal forms and directed toward a unification of the ultimate principle of "the One" with the diverse phenomena of "the Many." This could also apply to the number field.
We contend that the Holotomes are such self-contained models of holistic, self-reflective, finite portions of the number continuum. Holotomes are geometrically symmetrical, modular unities, or fractal sets which are based on the minimal numbers divisible by the the maximal factors of division. Each holotome adds an additional factor of divisibility to its circular unity. All base digits are captured by the number 2520.
ALSO SEE RUSSELL KRAMER SITE: http://bi-radialmatrix.weebly.com/

Russell Kramer is one of the core SYNDEX researchers and graphic artists, and that work has led him into deeper waters:
My name is Russell Kramer and I'm "discovering" the Bi-Radial Matrix. It is a continual process of unfolding into what appears to be the underlying geometry of nature even of space-time itself and its subsequent representation using geometric modeling. It is a cross section of something much vaster than can be thoroughly depicted by the models being employed. This is an ongoing investigation and search into the relationship between geometry and the basic elements of creation: space and time. Kramer demonstrates that space and time have geometric components which combine to form a harmonic structure on both the microscopic and macroscopic level. The universe is harmony on its most basic level.
There are key applications to the Bi-Radial Matrix:
1) Educational. The Bi-Radial Matrix deals with geometric and trigometric relations, along with coordinate systems and shows these concepts with visual clarity.
2) Geometric modeling of physical systems. The Bi-Radial Matrix is a highly useful model of Bi-Radial symmetry found in nature including atomic structure, electromagnetic and gravitational fields.The Bi-Radial Matrix shows the geometric origins of quantum potentials, "force" and "force fields"
3) Clean energy It is my belief that"nuclear" energy is an incomplete process, with radioactive byproducts, resulting from an incomplete understanding of the atom and the misapplication of technology to harness it. The Bi-Radial Matrix and further generalizations by indicating more details of atomic structure offers clues on how to harness the atom by more efficient process. As well the harmonic structure of space time itself offers the potential for limitless clean energy.
My name is Russell Kramer and I'm "discovering" the Bi-Radial Matrix. It is a continual process of unfolding into what appears to be the underlying geometry of nature even of space-time itself and its subsequent representation using geometric modeling. It is a cross section of something much vaster than can be thoroughly depicted by the models being employed. This is an ongoing investigation and search into the relationship between geometry and the basic elements of creation: space and time. Kramer demonstrates that space and time have geometric components which combine to form a harmonic structure on both the microscopic and macroscopic level. The universe is harmony on its most basic level.
There are key applications to the Bi-Radial Matrix:
1) Educational. The Bi-Radial Matrix deals with geometric and trigometric relations, along with coordinate systems and shows these concepts with visual clarity.
2) Geometric modeling of physical systems. The Bi-Radial Matrix is a highly useful model of Bi-Radial symmetry found in nature including atomic structure, electromagnetic and gravitational fields.The Bi-Radial Matrix shows the geometric origins of quantum potentials, "force" and "force fields"
3) Clean energy It is my belief that"nuclear" energy is an incomplete process, with radioactive byproducts, resulting from an incomplete understanding of the atom and the misapplication of technology to harness it. The Bi-Radial Matrix and further generalizations by indicating more details of atomic structure offers clues on how to harness the atom by more efficient process. As well the harmonic structure of space time itself offers the potential for limitless clean energy.
SYNDEX E-BOOKS & WEBSITES - Mandalog 2520 & 108

THE SYNERGETIC GEOMETRY OF NUMBER
There is a relationship between number dynamics and geometry that is pre-arithmatical, pre-mathematical. SYNDEX encodes the maximal amount of information in the minimal amount of graphic elements, disclosing circular unity in the natural geometry of number and a basewave in the natural number system. Circular Unity is the basis of Ancient Metrology & Number Dynamics.
Your cyclic synchrographing work clarifies and simplifies this whole matter to an epochal degree. At any rate, your work fills me with joy. Would you be willing to have me publish this work in another edition of SYNERGETICS with full credit to you?" --Buckminster Fuller to Bob Marshall, 1981
"...the powers of human reason could not be limited to any accepted prearranged system of formalized rules. What Godel showed was how to transcend any such system of rules, as long as those rules themselves could be trusted." --Roger Penrose
VIDEOS: Bob Marshall on SYNDEX basics
http://www.vimeo.com/11029460
http://www.vimeo.com/11213103
http://www.vimeo.com/11405292
TEXT & GRAPHICS
http://syndex1.iwarp.com/
http://syndex2.iwarp.com/
Syndex I & II are about the spiritual and universal beauty of numbers. They reflect the order and beauty of nature, but also of psyche. According to Jung, number unifies the physical and psychic (as in "realm of the psyche", not fortunetelling) worlds through synchronicity. Jung's basic ideas about the unity of knowledge and existence are in principle synonymous with the Platonic tradition, alchemy, Qabala and Gnosticism.
Plato treated the end product of the evolution of mathematical concepts, (a fixed system of idealized objects), as an independent beginning point of the evolution of the "world of things." This concrete form of philosophy was determined by the nature of Greek mathematics. These philosophies seek to reconcile the actual condition with a hypothetical distant ideal, which expansively incorporates both personal and universal dimensions. It is an inward-oriented epistemology.
By intuitive perception we can consciously reiterate the laws of Nature and mind which are equivalent to the archetypes themselves. Belief in the essential aspect of the mathematical as a real world, a "last reality" underlies the surprising efficiency of mathematics in the natural sciences and technology. But are numbers really abstract entities existing independently of the human mind? What is the nature of mathematical truth, and how is it translated into mathematical knowledge?
If it exists in another "ideal world", how can we know anything at all about the subject-matter of mathematics? What collective criteria determines the nature, terms and rules of this world? In the Jungian view, numbers (like other archetypes of the collective unconscious) are contents and patterns of behavior which are not personally acquired in experience but are inborn. The Platonic Forms are the objects of knowledge, which is regarded as innate. They can emerge dynamically as well as imagistically.
The essential nature of the Forms is dual: unity and multiplicity, finitude and infinitude. "The One" is the origin of Forms in the same way that the psyche is the origin of the archetypes. Because they form a primary conceptual language, numbers have heavily influenced the development of culture, philosophy and myth as well as sciences such as cosmology. 'Number is All' was the Pythagorean motto. Numbers were symbols representing cosmic principles. The whole philosophy of numbers came from distinctions created by the primordial division of the One into multiplicity. Because of their archetypal essence, their mode of articulation is essentially mythic and radically symbolic. Mathematics, by the very nature of its method, is an essentially Platonic pursuit.
Mathematicians treat the objects of their investigations as real objects in a hypostasized space, as if they existed independently in some pure world of their own. Thus, they reason that the amount of prime numbers is "infinite." Discussing the amount of prime numbers, mathematicians believe that they are discussing objects as real as collections of things in their everyday life.
We use numbers casually and rigorously as a language to order space. Since ancient times, their archetypal dynamics have been the foundation of philosophy, religious, and artistic thought. Patterns of dynamic energy in numbers reflect patterns of nature--the order of the universe. Whether they actually form the basis of the universe is the subject of ongoing debate among many schools of mathematicians. The qualitative distinctions we make between phenomena are fundamentally numerical.
We still don't know why the universe appears to follow mathematical laws. However, as Hilbert has suggested, we do know that the idea of the Infinite deviates significantly from the situation in the physical Universe. Are numbers and functions the inventions of mathematicians, or do they exist independently of us? Just because a mathematical object can possibly exist doesn't mean it actually does exist.
Yet, mathematicians imagine they are talking about real objects, when they may be talking about stabilized concepts. The new direction in the philosophy of mathematics is a "quasi-empirical approach that treats mathematics as just another messy experimental science." A partially unconscious process of idealization ends in the stable concept of numbers, points, lines, spheres. When working in geometry, a mathematician does not investigate the relations of real things. He investigates some idealized, fixed notion of these relations.
This notion is subjectively treated as "reality" without any fundamental reality behind it. It can, therefore, arguably be considered art as well as science. In practice, mathematicians jump to conclusions, and after the jump has been made begin the labor of proving the theorem or constructing a coherent theory. This involves subconscious reasoning, tenacity, focus, judgment, concentration, elementary intuition, free association, and conceptual visualization.
Some say mathematics is a purely human construct, an artifact of our nervous systems and culture. Others attest that even chimps and infants are hard-wired by evolution for arithmetic to deal with real objects in the real world. Numbers are not Platonic ideals but neurological creations. Integers, like colors, are artifacts of our sensory processing mechanisms. Dehaene traces the arithmetical model to the inferior parietal cortex. This poorly understood location is where visual, auditory, tactile signals, and language processing converge. Mathematics, or at least mathematical notation, is another human languge. It also appears to be the language of nature, and therefore physical reality.
Of the infinite range of mathematical creations, scientists keep those that help explain and predict reality. The concept of natural numbers is a fixed model, an idealization of quantitative relations which ends in stable concepts of numbers. The dynamics of those numbers are described in number theory, but SYNDEX describes number dynamics, not a theory or model, but a basewave in natural numbers. Number theory, one of the oldest branches of pure mathematics, concerns elementary properties of primes, divisibility among integers, the existence of greatest common divisors, the study of specific families of numbers, simple recurrent relations, factorization, and more.
Syndex addresses these aspects with easy to state conjectures which can be understood and observed in graphics without any particular mathematical training. Mathematical Platonism concerns the investigation of fixed or self-contained models. The Platonic Idea or Form is essentially an unchangeable form. As symbols, numbers express the particular in the universal, the eternal in the finite. They express the ordering function of their archetypal nature. The Neoplatonists assumed an a priori structure of knowledge grounded in archetypal forms and directed toward a unification of the ultimate principle of "the One" with the diverse phenomena of "the Many." This could also apply to the number field.
We contend that the Holotomes are such self-contained models of holistic, self-reflective, finite portions of the number continuum. Holotomes are geometrically symmetrical, modular unities, based on the minimal numbers divisible by the the maximal factors of division. Each holotome adds an additional factor of divisibility to its circular unity. All base digits are captured by the number 2520. Every subsequent holotome retains a copy of the initial data plus an additional factor.
Each holotome contains a rational section of a complete cycle. In these geometrical entities, the prime numbers are distributed in perfect radial symmetry within the context of every holotome. Such closed loops of causation are 'objective,' i.e. considered legitimate objects of scientific scrutiny. Number and geometry are two ways of expressing the same set of ratios or relationships. The Exemplary 9/11 Basewave (Cycloflex) is also a synergetic, dynamic representation of objective closed loops of causation. They can not only be described, but also graphically displayed. This is a reflexive +4, -4 ambidirectional base wave with a ninth null event, (as per Buckminster Fuller), forming a series of octaves running through the continuum.
This octave is a cyclic function. This base wave can be faithfully mapped into a single coherent syntactic time frame. The base wave is highlighted by palindromes and transpalindromes (the reverse identity of any number over a single digit, i.e. 16 - 61). Syntactic objects, which clearly exist represent similarly "real" objects--objects of investigation. Syndex is a method of mapping number structure and dynamic, synergetic behavior making number theory visibly coherent It geometrically paraphrases the elements of numeric progression. Syndex reveals the self-reflexive, synergetic properties of the base-10 natural number continuum or field. It simply exists at the level of nodes and mappings in the Syndex diagrams.
Syndex graphically displays formerly undiscovered symmetries in the natural number sequence and distribution of primes. It is based on a series of circular unities (self-contained objects), the results of prime number multiplexing, from whose factors cascade the whole panoply of ancient “sacred numbers” of many diverse cultures.
These sacred numbers come from the ancient wisdom traditions, including those of Sumeria, Babylonia, Egypt, the Bible, Plato, Pythagoras, ancient India, Stonehenge, the Mayans, and Qabala. Their importance to human culture echoes down to us from the past, not in any occult way, but by disclosing an ancient number canon that conceals and reveals inherent rhythms in the base-10 continuum. It reveals a synergetic relationship between number and geometry, which can be displayed graphically and easily understood even by the nonmathematical. These circularities are based on prime number multiplexing.
Within each circular number wheel, the primes are dispersed in rational, symmetrical deployment. This mandalic science helps us visualize facts about dynamic aspects of the interaction of numbers and their families. This fact remains undiscovered in classical number theory, and is discussed under the rubric of the prime number enigma.
The Auric Key to this enigma is the rediscovery of the original program of the alphanumeric system of notation and the fundamental platform of general science, the history of which began with horizon-based astronomy and cosmology in Sumeria. The Auric Key excavates many vital properties of numbers. Classical cultures are characterized by certain basic ideas, of which metrology is foremost.
Ancient metrology was a system of interlinked measures, numeration, astronomical cycles, and geodetic standards. We can find the most often cited numbers of ancient metrology extrapolating out of a certain numerical sequence, (The Holotomic Sequence). We begin with the question of why some unknown and ancient geometer selected 360 degrees for dividing the celestial sphere and the circle.
The division of 360 by 12 produced one of the first historical cosmologies--the Zodiac. The basis of this standard of circular unity can be deduced. 360 is divisible by all eight base digits except the number 7. To include 7 as a divisor, the prime circular module must be raised to 2520, the Auric Key, the lowest number divisible by all base digits.
From this clue, we can destrapolate and extrapolate an essential sequence, a family of numbers. It turns out that 360 is but one in a strategic series of circular unities based on prime number multiplexing. Numbers 2, 3, 5, 7, 11, and 13 are the first primes. By starting with 6 (the first perfect number) and multiplying by the primes in their natural order, we get the sequence 12, 24, 72, 360, 2520, 27720, 360360, 6126120, etc.
Each of these numbers forms a geometrical entity, a circular unity, (Holotome). These numbers just happen to be the exact sequence of minimal sums that accomodate the maximal amount of factors of division. Their synergetic qualities have remained unnoticed in classical number theory. This minimalism is reflected in Syndex number theory. The first concern of Syndex method is to encode the maximum information expressed through minimal graphic elements.
Therefore, we employ correspondences between numbers, colors, and frequencies of divisibility to integrate the system. The number 2520 is the Auric Key. It, not 360, is the first number divisible by all nine base digits. It is exactly twice the number 1260, a number referred to cabalistically five times in the Book of Revelations (12:6 and 12:4). It is half of the number 5040, which figures prominently in Plato’s “Laws” regarding his ideal city/state.
This number 2520, more than 360, captures nature’s cyclic behaviors. And the graphic number wheel (synchrograph or mandalog) based on this number reverses to form a mirror image of itself at the midpoint of 1260. The real key involves the sequence in which prime numbers naturally occur in the base-10 continuum. This synergetic effect is demonstrated by multiplying the third and fourth Holotomes together: 72 x 360 = 25920, a number given for the Precession of the Equinoxes in Sumerian cuneiform records.
In Sumeria, mathematics was based on a sexagesimal system (60s) with a decimal substrate (10s). The Sumerian sar was based on multiples of 36, 360, 3600; it was known as the number of the Universe (36 x 10 = 360). Imagine a circle for space of 360 degrees x 60 minutes x 60 seconds = 1,296,000 seconds. The real key to this system involves the sequence in which prime numbers naturally occur in the base-10 continuum: 72 x 360 = 25920 divided by 2 = 12960; divided by 3 = 8640; divided by 4 = 6480; divided by 6 = 4320. 72 + 360 = 432.
The precessional number, 25920, can also be arrived at by 432 x 60 = 25920, employing the Sumerian sexagesimal system. This number relates directly to ancient Hindu cosmology and divine time measurement as the Ages and Yugas. Their numbers (without the cosmological zeros) include 432, 864, 1296, 1728, 4320 for the Yugas, and 648, 1296, 1944, 2592, 6480 for the Ages. Both Ages and Yugas share the number 1296 (362). The Hindu systems are based on multiples of #108 (3 x 36), the divine numberword OM, also known as the number of the Universe. The Yugas and Ages can also be generated on multiples of 36. Multiply by 12, 24, 36, and 48 for the Yugas; and 18, 36, 54, and 72 for the Ages. 12960 (half the Precessional cycle) is a numerical basis for astronomical measures and played a role in Plato's mystic symbolism: 12 x 2160 (Platonic Month) = 25920 (Platonic Year).
In all cases, the historical precedent for this system comes from Sumeria, and its ancient cosmology inspired by horizon-based astronomy. These numbers and their importance come from direct observation of the precessional cycle and orbital times of the planets. Ancient India raised mathematics and astronomy to a fine art. In medieval times, it gave the west its system of so-called Arabic numerals, the base-10 system, place value, and the zero, and created a Renaissance in art and science. It is within this system of mathematical notation that the +4, -4 basewave inherent in the continuum can most easily be seen through the mechanism of palindromes and transpalindromes.
SYNDEX I identifies and demonstrates the various properties of the base-10 number field, such as the symmetrical distribution of prime numbers. The continuum can be viewed as both progressive and regressive, or self-reflexive. The key to the comprehensive analysis of general number behavior is found in the concept of "circular unity." The graphic importance of the Holotomic Sequence is that circular symmetry is being conserved and may be enlisted as the fundamental reference key in the graphic investigations of number behavior.
The primes are deployed in symmetrical interface only within these specific Holotomic domains. Synchrographics regards symmetry as a primary analytical reference, making the Syndex archetypal system of number classes possible. The foundation of this system is palindromes and transpalindromes, yielding 12 classes of number. Palindromes, or binomial reflection numbers are neither purely accidental nor without significance.
Transpalindromes are the reversal of any particular number exceeding a single digit. Numeronomy, the laws relating to the essential structure and dynamics of number, is a new word for an extremely ancient science. This science, (based on the knowledge that the continuum contains a definite structural order with general laws that describe the nature of that order), has laws that relate to the general behavior of nature itself. Each number has both a geometrical and numerical identity.
The outcome of Synchrographics is that numbers speak for themselves through structure and synergetic behavior. All Syndex mandalogs (number wheels) are the product of the systematic generation of the exact sequence of minimax factorization. They have the perfect retrograde feature by which the patterns generated in the first half of the spiral are reversed at midpoint and are reflected as a mirrored image in the second half of the spiral. Revisioning the number continuum with the concept of simultaneous counterflow yields a more accurate picture. This revisioning is also happening in post-quantum physics under the rubric of quantum backflow. With large spans of numbers, the complex interrelationships become difficult to visualize without good graphics.
Because of the octave nature of the base cycle, there cannot be more than four consecutive transpalindromic pairs in a single symmetrical sequence, regardless of the amount of digits in each individual number. The Holotomic Sequence consists of a series of key numbers or circular unities in the rhythmic wave. Buckminster Fuller was very excited and "filled with joy" over these revelations, when the Syndex discoveries were shared with him before his death. He wanted to publish them in a subsequent edition of Synergetics. And why not, since they shed light on old enigmas. After all, numbers are what they are, not what we wish them to be. They will not do what they cannot do, i.e. show symmetries where none exist.
SYNDEX II is about the process of discovering synergetic, rhythmic symmetries on a graphic enspiralment called Synchrograph C. It is based on the Hindu number of the Universe, 108. On this number wheel, the natural numbers are spiralled 60 times around a radial array of 108 increments to the number 6480. Contemplating the C-Graph over the years has produced several revelations, including the Holotomic Sequence, created by prime number multiplexing, and the exemplary 9/11 wave cycle (a +4, -4 base wave). On Synchrograph C all the numbers that represent the two Hindu astrocalendaric systems fall in the same zero axis. The sum of the Yugas falls at 2/3 of this axis. 6480 divided by 3 = 2160, the Platonic Month; 12 x 2160 = 25920, Platonic Year.
On this graph the four-digit palindromic sequence (1881, 2772, 3663, 4554) appears in quadratic array, where only chaos exists in classical number theory. Jung asserted that number forms the particular element which unites the realms of psyche and matter. It is real in an archetypal, qualitative sense and a quantitative sense, uniting the imaginal and the physically knowable. The psychic dynamics of the concept of number appear archetypally as its "transgressive" aspect in the realm of matter.
Numbers above the threshold of consciousness appear as quantitative discontinuities and qualitative individual numbers. But according to the Jungians, in the unconscious they interpermeate and overlap participating in the one continuum that runs through them all. Thus, we find certain synchronicities in the Syndex numberwheel mandalas, creating metaphysical and empirical harmonies. Certain authentic mathematical structures can originate in the unconscious even though Western number theory has traditionally followed a very different path, using its accepted, formalized rules.
On rare occasions graphical architecture combines with the data content to yield a uniquely spectacular graphic. Such entities caqn be described and admired but there are no compositional principles on how to create that one wonderful graphic in a million. The ultimate Platonic ideal was that of Beauty. The most beautiful graphics do not traffic with the trivial. Graphical elegance is often found in simplicity of design and complexity of data. Visually attractive graphics also gather their power for content and interpretations beyond the immediate display of some numbers. The best graphics are about the useful and important, about life and death, about the universe.
SYNDEX 2: number mysticism and alphanumeric writing; cosmic cycles of creation and destruction (Yugas and Ages); ancient Hindu mathematics & astronomy; mandalog #108; the Sumerian legacy; models of sacred space; milestones in the evolution of the number concept; Syndex number theory; metrology; cosmography.
http://syndex2.iwarp.com/
http://syndex1.iwarp.com/
Below: 2520 Ultrasynch Mandalog by Russell Kramer
Mandalog

[2520 Mandalog]
Every subsequent holotome retains a copy of the initial data plus an additional factor. Each holotome contains a rational section of a complete cycle. In these geometrical entities, the prime numbers are distributed in perfect radial symmetry within the context of every holotome. Such closed loops of causation are 'objective,' i.e. considered legitimate objects of scientific scrutiny.
Number and geometry are two ways of expressing the same set of ratios or relationships. The Exemplary 9/11 Basewave (Cycloflex) is also a synergetic, dynamic representation of objective closed loops of causation. They can not only be described, but also graphically displayed. This is a reflexive +4, -4 ambidirectional base wave with a ninth null event, (as per Buckminster Fuller), forming a series of octaves running through the continuum.
This octave is a cyclic function. This base wave can be faithfully mapped into a single coherent syntactic time frame. The base wave is highlighted by palindromes and transpalindromes (the reverse identity of any number over a single digit, i.e. 16 - 61). Syntactic objects, which clearly exist represent similarly "real" objects--objects of investigation.
Syndex is a method of mapping number structure and dynamic, synergetic behavior making number theory visibly coherent It geometrically paraphrases the elements of numeric progression. Syndex reveals the self-reflexive, synergetic properties of the base-10 natural number continuum or field. It simply exists at the level of nodes and mappings in the Syndex diagrams.
Syndex graphically displays formerly undiscovered symmetries in the natural number sequence and distribution of primes. It is based on a series of circular unities (self-contained objects), the results of prime number multiplexing, from whose factors cascade the whole panoply of ancient “sacred numbers” of many diverse cultures.
These sacred numbers come from the ancient wisdom traditions, including those of Sumeria, Babylonia, Egypt, the Bible, Plato, Pythagoras, ancient India, Stonehenge, the Mayans, and Qabala. Their importance to human culture echoes down to us from the past, not in any occult way, but by disclosing an ancient number canon that conceals and reveals inherent rhythms in the base-10 continuum. It reveals a synergetic relationship between number and geometry, which can be displayed graphically and easily understood even by the nonmathematical.
These circularities are based on prime number multiplexing. Within each circular number wheel, the primes are dispersed in rational, symmetrical deployment. This mandalic science helps us visualize facts about dynamic aspects of the interaction of numbers and their families. This fact remains undiscovered in classical number theory, and is discussed under the rubric of the prime number enigma.
The Auric Key to this enigma is the rediscovery of the original program of the alphanumeric system of notation and the fundamental platform of general science, the history of which began with horizon-based astronomy and cosmology in Sumeria. The Auric Key excavates many vital properties of numbers.
Classical cultures are characterized by certain basic ideas, of which metrology is foremost. Ancient metrology was a system of interlinked measures, numeration, astronomical cycles, and geodetic standards. We can find the most often cited numbers of ancient metrology extrapolating out of a certain numerical sequence, (The Holotomic Sequence).
We begin with the question of why some unknown and ancient geometer selected 360 degrees for dividing the celestial sphere and the circle. The division of 360 by 12 produced one of the first historical cosmologies--the Zodiac. The basis of this standard of circular unity can be deduced.
360 is divisible by all eight base digits except the number 7. To include 7 as a divisor, the prime circular module must be raised to 2520, the Auric Key, the lowest number divisible by all base digits. From this clue, we can destrapolate and extrapolate an essential sequence, a family of numbers.
It turns out that 360 is but one in a strategic series of circular unities based on prime number multiplexing. Numbers 2, 3, 5, 7, 11, and 13 are the first primes. By starting with 6 (the first perfect number) and multiplying by the primes in their natural order, we get the sequence12, 24, 72, 360, 2520, 27720, 360360, 6126120, etc. Each of these numbers forms a geometrical entity, a circular unity, (Holotome). These numbers just happen to be the exact sequence of minimal sums that accomodate the maximal amount of factors of division. Their synergetic qualities have remained unnoticed in classical number theory.
This minimalism is reflected in Syndex number theory. The first concern of Syndex method is to encode the maximum information expressed through minimal graphic elements. Therefore, we employ correspondences between numbers, colors, and frequencies of divisibility to integrate the system.
The number 2520 is the Auric Key. It, not 360, is the first number divisible by all nine base digits. It is exactly twice the number 1260, a number referred to cabalistically five times in the Book of Revelations (12:6 and 12:4). It is half of the number 5040, which figures prominently in Plato’s “Laws” regarding his ideal city/state.
This number 2520, more than 360, captures nature’s cyclic behaviors. And the graphic number wheel (synchrograph or mandalog) based on this number reverses to form a mirror image of itself at the midpoint of 1260. The real key involves the sequence in which prime numbers naturally occur in the base-10 continuum.
This synergetic effect is demonstrated by multiplying the third and fourth Holotomes together: 72 x 360 = 25920, a number given for the Precession of the Equinoxes in Sumerian cuneiform records. In Sumeria, mathematics was based on a sexagesimal system (60s) with a decimal substrate (10s). The Sumerian sar was based on multiples of 36, 360, 3600; it was known as the number of the Universe (36 x 10 = 360). Imagine a circle for space of 360 degrees x 60 minutes x 60 seconds = 1,296,000 seconds.
The real key to this system involves the sequence in which prime numbers naturally occur in the base-10 continuum:
72 x 360 = 25920 divided by 2 = 12960; divided by 3 = 8640; divided by 4 = 6480; divided by 6 = 4320. 72 + 360 = 432.
The precessional number, 25920, can also be arrived at by 432 x 60 = 25920, employing the Sumerian sexagesimal system. This number relates directly to ancient Hindu cosmology and divine time measurement as the Ages and Yugas. Their numbers (without the cosmological zeros) include 432, 864, 1296, 1728, 4320 for the Yugas, and 648, 1296, 1944, 2592, 6480 for the Ages.Both Ages and Yugas share the number 1296 (362).
The Hindu systems are based on multiples of #108 (3 x 36), the divine numberword OM, also known as the number of the Universe. The Yugas and Ages can also be generated on multiples of 36. Multiply by 12, 24, 36, and 48 for the Yugas; and 18, 36, 54, and 72 for the Ages.
12960 (half the Precessional cycle) is a numerical basis for astronomical measures and played a role in Plato's mystic symbolism: 12 x 2160 (Platonic Month) = 25920 (Platonic Year). In all cases, the historical precedent for this system comes from Sumeria, and its ancient cosmology inspired by horizon-based astronomy. These numbers and their importance come from direct observation of the precessional cycle and orbital times of the planets.
Ancient India raised mathematics and astronomy to a fine art. In medieval times, it gave the west its system of so-called Arabic numerals, the base-10 system, place value, and the zero, and created a Renaissance in art and science. It is within this system of mathematical notation that the +4, -4 basewave inherent in the continuum can most easily be seen through the mechanism of palindromes and transpalindromes.
SYNDEX I identifies and demonstrates the various properties of the base-10 number field, such as the symmetrical distribution of prime numbers. The continuum can be viewed as both progressive and regressive, or self-reflexive. The key to the comprehensive analysis of general number behavior is found in the concept of "circular unity." The graphic importance of the Holotomic Sequence is that circular symmetry is being conserved and may be enlisted as the fundamental reference key in the graphic investigations of number behavior. The primes are deployed in symmetrical interface only within these specific Holotomic domains.
Synchrographics regards symmetry as a primary analytical reference, making the Syndex archetypal system of number classes possible. The foundation of this system is palindromes and transpalindromes, yielding 12 classes of number. Palindromes, or binomial reflection numbers are neither purely accidental nor without significance. Transpalindromes are the reversal of any particular number exceeding a single digit.
Numeronomy, the laws relating to the essential structure and dynamics of number, is a new word for an extremely ancient science. This science, (based on the knowledge that the continuum contains a definite structural order with general laws that describe the nature of that order), has laws that relate to the general behavior of nature itself. Each number has both a geometrical and numerical identity. The outcome of Synchrographics is that numbers speak for themselves through structure and synergetic behavior.
All Syndex mandalogs (number wheels) are the product of the systematic generation of the exact sequence of minimax factorization. They have the perfect retrograde feature by which the patterns generated in the first half of the spiral are reversed at midpoint and are reflected as a mirrored image in the second half of the spiral. Revisioning the number continuum with the concept of simultaneous counterflow yields a more accurate picture. This revisioning is also happening in post-quantum physics under the rubric of quantum backflow.
With large spans of numbers, the complex interrelationships become difficult to visualize without good graphics. Because of the octave nature of the base cycle, there cannot be more than four consecutive transpalindromic pairs in a single symmetrical sequence, regardless of the amount of digits in each individual number. The Holotomic Sequence consists of a series of key numbers or circular unities in the rhythmic wave.
Buckminster Fuller was very excited and "filled with joy" over these revelations, when the Syndex discoveries were shared with him before his death. He wanted to publish them in a subsequent edition of Synergetics. And why not, since they shed light on old enigmas. After all, numbers are what they are, not what we wish them to be. They will not do what they cannot do, i.e. show symmetries where none exist.
SYNDEX II is about the process of discovering synergetic, rhythmic symmetries on a graphic enspiralment called Synchrograph C. It is based on the Hindu number of the Universe, 108. On this number wheel, the natural numbers are spiralled 60 times around a radial array of 108 increments to the number 6480. Contemplating the C-Graph over the years has produced several revelations, including the Holotomic Sequence, created by prime number multiplexing, and the exemplary 9/11 wave cycle (a +4, -4 base wave).
On Synchrograph C all the numbers that represent the two Hindu astrocalendaric systems fall in the same zero axis. The sum of the Yugas falls at 2/3 of this axis. 6480 divided by 3 = 2160, the Platonic Month; 12 x 2160 = 25920, Platonic Year. On this graph the four-digit palindromic sequence (1881, 2772, 3663, 4554) appears in quadratic array, where only chaos exists in classical number theory.
Jung asserted that number forms the particular element which unites the realms of psyche and matter. It is real in an archetypal, qualitative sense and a quantitative sense, uniting the imaginal and the physically knowable. The psychic dynamics of the concept of number appear archetypally as its "transgressive" aspect in the realm of matter. Numbers above the threshold of consciousness appear as quantitative discontinuities and qualitative individual numbers. But according to the Jungians, in the unconscious they interpermeate and overlap participating in the one continuum that runs through them all.
Thus, we find certain synchronicities in the Syndex numberwheel mandalas, creating metaphysical and empirical harmonies. Certain authentic mathematical structures can originate in the unconscious even though Western number theory has traditionally followed a very different path, using its accepted, formalized rules. On rare occasions graphical architecture combines with the data content to yield a uniquely spectacular graphic. Such entities caqn be described and admired but there are no compositional principles on how to create that one wonderful graphic in a million.
The ultimate Platonic ideal was that of Beauty. The most beautiful graphics do not traffic with the trivial. Graphical elegance is often found in simplicity of design and complexity of data. Visually attractive graphics also gather their power for content and interpretations beyond the immediate display of some numbers. The best graphics are about the useful and important, about life and death, about the universe.
"2520: The Auric Key"
SYNDEX I : contains more on Synergetics and Qabala, magick, Stonehenge, ancient insight. The Diamond Body: Buckminster Fuller and the Qabala; N = 50, V = 6; Music of the Spheres; Number and Jung's Transformational Process; The Auric Key; Numeronomy and Synchrographics.
SYNDEX II : number mysticism and alphanumeric writing; cosmic cycles of creation and destruction (Yugas and Ages); ancient Hindu mathematics & astronomy; mandalog #108; the Sumerian legacy; models of sacred space; milestones in the evolution of the number concept; Syndex number theory; metrology; cosmography.
Every subsequent holotome retains a copy of the initial data plus an additional factor. Each holotome contains a rational section of a complete cycle. In these geometrical entities, the prime numbers are distributed in perfect radial symmetry within the context of every holotome. Such closed loops of causation are 'objective,' i.e. considered legitimate objects of scientific scrutiny.
Number and geometry are two ways of expressing the same set of ratios or relationships. The Exemplary 9/11 Basewave (Cycloflex) is also a synergetic, dynamic representation of objective closed loops of causation. They can not only be described, but also graphically displayed. This is a reflexive +4, -4 ambidirectional base wave with a ninth null event, (as per Buckminster Fuller), forming a series of octaves running through the continuum.
This octave is a cyclic function. This base wave can be faithfully mapped into a single coherent syntactic time frame. The base wave is highlighted by palindromes and transpalindromes (the reverse identity of any number over a single digit, i.e. 16 - 61). Syntactic objects, which clearly exist represent similarly "real" objects--objects of investigation.
Syndex is a method of mapping number structure and dynamic, synergetic behavior making number theory visibly coherent It geometrically paraphrases the elements of numeric progression. Syndex reveals the self-reflexive, synergetic properties of the base-10 natural number continuum or field. It simply exists at the level of nodes and mappings in the Syndex diagrams.
Syndex graphically displays formerly undiscovered symmetries in the natural number sequence and distribution of primes. It is based on a series of circular unities (self-contained objects), the results of prime number multiplexing, from whose factors cascade the whole panoply of ancient “sacred numbers” of many diverse cultures.
These sacred numbers come from the ancient wisdom traditions, including those of Sumeria, Babylonia, Egypt, the Bible, Plato, Pythagoras, ancient India, Stonehenge, the Mayans, and Qabala. Their importance to human culture echoes down to us from the past, not in any occult way, but by disclosing an ancient number canon that conceals and reveals inherent rhythms in the base-10 continuum. It reveals a synergetic relationship between number and geometry, which can be displayed graphically and easily understood even by the nonmathematical.
These circularities are based on prime number multiplexing. Within each circular number wheel, the primes are dispersed in rational, symmetrical deployment. This mandalic science helps us visualize facts about dynamic aspects of the interaction of numbers and their families. This fact remains undiscovered in classical number theory, and is discussed under the rubric of the prime number enigma.
The Auric Key to this enigma is the rediscovery of the original program of the alphanumeric system of notation and the fundamental platform of general science, the history of which began with horizon-based astronomy and cosmology in Sumeria. The Auric Key excavates many vital properties of numbers.
Classical cultures are characterized by certain basic ideas, of which metrology is foremost. Ancient metrology was a system of interlinked measures, numeration, astronomical cycles, and geodetic standards. We can find the most often cited numbers of ancient metrology extrapolating out of a certain numerical sequence, (The Holotomic Sequence).
We begin with the question of why some unknown and ancient geometer selected 360 degrees for dividing the celestial sphere and the circle. The division of 360 by 12 produced one of the first historical cosmologies--the Zodiac. The basis of this standard of circular unity can be deduced.
360 is divisible by all eight base digits except the number 7. To include 7 as a divisor, the prime circular module must be raised to 2520, the Auric Key, the lowest number divisible by all base digits. From this clue, we can destrapolate and extrapolate an essential sequence, a family of numbers.
It turns out that 360 is but one in a strategic series of circular unities based on prime number multiplexing. Numbers 2, 3, 5, 7, 11, and 13 are the first primes. By starting with 6 (the first perfect number) and multiplying by the primes in their natural order, we get the sequence12, 24, 72, 360, 2520, 27720, 360360, 6126120, etc. Each of these numbers forms a geometrical entity, a circular unity, (Holotome). These numbers just happen to be the exact sequence of minimal sums that accomodate the maximal amount of factors of division. Their synergetic qualities have remained unnoticed in classical number theory.
This minimalism is reflected in Syndex number theory. The first concern of Syndex method is to encode the maximum information expressed through minimal graphic elements. Therefore, we employ correspondences between numbers, colors, and frequencies of divisibility to integrate the system.
The number 2520 is the Auric Key. It, not 360, is the first number divisible by all nine base digits. It is exactly twice the number 1260, a number referred to cabalistically five times in the Book of Revelations (12:6 and 12:4). It is half of the number 5040, which figures prominently in Plato’s “Laws” regarding his ideal city/state.
This number 2520, more than 360, captures nature’s cyclic behaviors. And the graphic number wheel (synchrograph or mandalog) based on this number reverses to form a mirror image of itself at the midpoint of 1260. The real key involves the sequence in which prime numbers naturally occur in the base-10 continuum.
This synergetic effect is demonstrated by multiplying the third and fourth Holotomes together: 72 x 360 = 25920, a number given for the Precession of the Equinoxes in Sumerian cuneiform records. In Sumeria, mathematics was based on a sexagesimal system (60s) with a decimal substrate (10s). The Sumerian sar was based on multiples of 36, 360, 3600; it was known as the number of the Universe (36 x 10 = 360). Imagine a circle for space of 360 degrees x 60 minutes x 60 seconds = 1,296,000 seconds.
The real key to this system involves the sequence in which prime numbers naturally occur in the base-10 continuum:
72 x 360 = 25920 divided by 2 = 12960; divided by 3 = 8640; divided by 4 = 6480; divided by 6 = 4320. 72 + 360 = 432.
The precessional number, 25920, can also be arrived at by 432 x 60 = 25920, employing the Sumerian sexagesimal system. This number relates directly to ancient Hindu cosmology and divine time measurement as the Ages and Yugas. Their numbers (without the cosmological zeros) include 432, 864, 1296, 1728, 4320 for the Yugas, and 648, 1296, 1944, 2592, 6480 for the Ages.Both Ages and Yugas share the number 1296 (362).
The Hindu systems are based on multiples of #108 (3 x 36), the divine numberword OM, also known as the number of the Universe. The Yugas and Ages can also be generated on multiples of 36. Multiply by 12, 24, 36, and 48 for the Yugas; and 18, 36, 54, and 72 for the Ages.
12960 (half the Precessional cycle) is a numerical basis for astronomical measures and played a role in Plato's mystic symbolism: 12 x 2160 (Platonic Month) = 25920 (Platonic Year). In all cases, the historical precedent for this system comes from Sumeria, and its ancient cosmology inspired by horizon-based astronomy. These numbers and their importance come from direct observation of the precessional cycle and orbital times of the planets.
Ancient India raised mathematics and astronomy to a fine art. In medieval times, it gave the west its system of so-called Arabic numerals, the base-10 system, place value, and the zero, and created a Renaissance in art and science. It is within this system of mathematical notation that the +4, -4 basewave inherent in the continuum can most easily be seen through the mechanism of palindromes and transpalindromes.
SYNDEX I identifies and demonstrates the various properties of the base-10 number field, such as the symmetrical distribution of prime numbers. The continuum can be viewed as both progressive and regressive, or self-reflexive. The key to the comprehensive analysis of general number behavior is found in the concept of "circular unity." The graphic importance of the Holotomic Sequence is that circular symmetry is being conserved and may be enlisted as the fundamental reference key in the graphic investigations of number behavior. The primes are deployed in symmetrical interface only within these specific Holotomic domains.
Synchrographics regards symmetry as a primary analytical reference, making the Syndex archetypal system of number classes possible. The foundation of this system is palindromes and transpalindromes, yielding 12 classes of number. Palindromes, or binomial reflection numbers are neither purely accidental nor without significance. Transpalindromes are the reversal of any particular number exceeding a single digit.
Numeronomy, the laws relating to the essential structure and dynamics of number, is a new word for an extremely ancient science. This science, (based on the knowledge that the continuum contains a definite structural order with general laws that describe the nature of that order), has laws that relate to the general behavior of nature itself. Each number has both a geometrical and numerical identity. The outcome of Synchrographics is that numbers speak for themselves through structure and synergetic behavior.
All Syndex mandalogs (number wheels) are the product of the systematic generation of the exact sequence of minimax factorization. They have the perfect retrograde feature by which the patterns generated in the first half of the spiral are reversed at midpoint and are reflected as a mirrored image in the second half of the spiral. Revisioning the number continuum with the concept of simultaneous counterflow yields a more accurate picture. This revisioning is also happening in post-quantum physics under the rubric of quantum backflow.
With large spans of numbers, the complex interrelationships become difficult to visualize without good graphics. Because of the octave nature of the base cycle, there cannot be more than four consecutive transpalindromic pairs in a single symmetrical sequence, regardless of the amount of digits in each individual number. The Holotomic Sequence consists of a series of key numbers or circular unities in the rhythmic wave.
Buckminster Fuller was very excited and "filled with joy" over these revelations, when the Syndex discoveries were shared with him before his death. He wanted to publish them in a subsequent edition of Synergetics. And why not, since they shed light on old enigmas. After all, numbers are what they are, not what we wish them to be. They will not do what they cannot do, i.e. show symmetries where none exist.
SYNDEX II is about the process of discovering synergetic, rhythmic symmetries on a graphic enspiralment called Synchrograph C. It is based on the Hindu number of the Universe, 108. On this number wheel, the natural numbers are spiralled 60 times around a radial array of 108 increments to the number 6480. Contemplating the C-Graph over the years has produced several revelations, including the Holotomic Sequence, created by prime number multiplexing, and the exemplary 9/11 wave cycle (a +4, -4 base wave).
On Synchrograph C all the numbers that represent the two Hindu astrocalendaric systems fall in the same zero axis. The sum of the Yugas falls at 2/3 of this axis. 6480 divided by 3 = 2160, the Platonic Month; 12 x 2160 = 25920, Platonic Year. On this graph the four-digit palindromic sequence (1881, 2772, 3663, 4554) appears in quadratic array, where only chaos exists in classical number theory.
Jung asserted that number forms the particular element which unites the realms of psyche and matter. It is real in an archetypal, qualitative sense and a quantitative sense, uniting the imaginal and the physically knowable. The psychic dynamics of the concept of number appear archetypally as its "transgressive" aspect in the realm of matter. Numbers above the threshold of consciousness appear as quantitative discontinuities and qualitative individual numbers. But according to the Jungians, in the unconscious they interpermeate and overlap participating in the one continuum that runs through them all.
Thus, we find certain synchronicities in the Syndex numberwheel mandalas, creating metaphysical and empirical harmonies. Certain authentic mathematical structures can originate in the unconscious even though Western number theory has traditionally followed a very different path, using its accepted, formalized rules. On rare occasions graphical architecture combines with the data content to yield a uniquely spectacular graphic. Such entities caqn be described and admired but there are no compositional principles on how to create that one wonderful graphic in a million.
The ultimate Platonic ideal was that of Beauty. The most beautiful graphics do not traffic with the trivial. Graphical elegance is often found in simplicity of design and complexity of data. Visually attractive graphics also gather their power for content and interpretations beyond the immediate display of some numbers. The best graphics are about the useful and important, about life and death, about the universe.
"2520: The Auric Key"
SYNDEX I : contains more on Synergetics and Qabala, magick, Stonehenge, ancient insight. The Diamond Body: Buckminster Fuller and the Qabala; N = 50, V = 6; Music of the Spheres; Number and Jung's Transformational Process; The Auric Key; Numeronomy and Synchrographics.
SYNDEX II : number mysticism and alphanumeric writing; cosmic cycles of creation and destruction (Yugas and Ages); ancient Hindu mathematics & astronomy; mandalog #108; the Sumerian legacy; models of sacred space; milestones in the evolution of the number concept; Syndex number theory; metrology; cosmography.




